Beyond visualizing the mathematical concepts in pattern formation, you may be curious to learn about how the animations were actually implemented using MATLAB. In this section I want introduce some of the key ideas behind the code that was used to generate the animated gifs, guide you through some of the code, and make it accessible for you to make similar animations as well.

First, I will go through the (explicit and implicit) numerical solution of the 1D Heat Equation, and then I will step through the explicit numerical solution for a 2D Heat Equation.

Note: I assume that you are familiar with the Forward and Backward Euler Methods to solve ordinary differential equations.

Recall that the Heat equation (also the diffusion equation) is: $$\begin{equation} \label{heatEqn} \frac{\partial u}{\partial t}\, - \,D_u \frac{\partial ^2 u}{\partial x^2}\, =\, 0, \end{equation}$$ where $u$ is temperature, and $D_u$ is a constant that determines how fast heat spreads out. Before we go into the numerics let us step through the solution to the heat equation.

Imagine we have an insulated rod with initial condition $u(x,0) = u_0$ boundary conditions $u(x,t) = u(L,t) = 0$. We want to solve the PDE in Equation [$\ref{heatEqn}$]. The trick is to assume that the solutions are separable, so $$\begin{equation} \label{eqn:heatEqnsep1} u(x,t) = T(t)X(x) \end{equation}$$

We can substitute this solution into Equation [$\ref{heatEqn}$] to get $$\begin{equation} \label{eqn:heatEqnsep2} \underbrace{T'(t)X(x)}_{\Large =\frac{\partial u}{\partial t}} = D_u\underbrace{ T(t)X''(x)}_{\Large =\frac{\partial^2 u}{\partial x^2}}. \end{equation}$$

Rearranging terms we get

$$\begin{equation} \label{eqn:heatEqnsep3} \frac{ T'(t)}{D_u T(t)} = \frac{X''(x)}{X(x)}. \end{equation}$$

Note that the LHS (left hand side) is a function of time where the RHS (right hand side) is a function of position. In order for this equality to be satisfied for all $x$ and $t$, we must have that they are both equal to a constant. We let

$$\begin{equation} \label{eqn:heatEqnsep4} \frac{ T'(t)}{D_u T(t)} = \frac{X''(x)}{X(x)} = -\lambda^2 \text{, } \quad \lambda > 0. \end{equation}$$

Solving for each variable we get that $$\begin{align} T(t) &= Ae^{-\lambda^2 D_u t}\\ X(x) &= Bcos(\lambda x) + Csin(\lambda x) \end{align}$$

Here, $A$ is a positive real constant. We can apply our boundary conditions to find what $B$ and $C$ should be. Since the edges at $x=0$ is clamped at zero ($u(0,t)=0$), then $B=0$. The rod is also clamped at zero at $x=L$, and since $C\neq 0$, then $sin(\lambda L) =0$ This means that $\lambda_n = \frac{n\pi}{L}$ where $n\in \mathbb{Z}$.

Note that:

• $n=0$ give a trivial solution
• $n\in \mathbb{Z}^-$ just makes all the coefficients negative, so we can just consider the positive values of n.

As a result, we get the following eigenfunctions:

$$\begin{equation} \label{eqn:heatEqneigen1} u_n(x,t) =A_n e^{-\lambda_n^2 D_u t} sin(\lambda_n x) \text{, } \quad n=1,2,..., \end{equation}$$ with eigenvalues

$$\begin{equation} \label{eqn:heatEqneigen2} \lambda_n = \frac{n\pi}{L} \end{equation}$$

We are not done yet, because we still need to find the conditions s.t. we satisfy the initial conditions. Since linear combinations of solutions will still be solutions, then $$\begin{equation} \label{eqn:heatEqnfour1} u(x,t) = \sum_{n=1}^\infty A_n e^{-\lambda_n^2 D_u t} sin(\lambda_n x), \end{equation}$$ is still a solution. We would like it then, if we could express $u_0$ as a sum of sine functions as shown in Equation [$\ref{eqn:heatEqnfour1}$]. This is true for most $u_0$ and it is the theory of Fourier Series.

Although I will not get into the details here, it can be shown that the Fourier sine coefficients are:

$$\begin{equation} \label{eqn:heatEqneigen3} A_n = \frac{2}{L} \int_0^L u_0(x)sin(\lambda_n x) dx \end{equation}$$

However, in general, it is not always easy to obtain solutions to PDE's in closed form, and arguably even Equation $\eqref{eqn:heatEqneigen2}$ is not as easy to understand (unless you can visualize an infinite sum!). Instead, we turn to numerical simulations to Partial Differential equations. One of the methods used is known as the finite-difference method. (For a more complete discussion and more Matlab examples and exercises see [(kharab_2002)]).

One of the difficulties when numerically simulating the heat equation is that $\eqref{heatEqn}$ contains partial derivative in both time and space. We can approximate the partial derivatives of $u(x,t)$ in Eqn. $\eqref{heatEqn}$ as follows: $$\begin{gather} \label{eqn:uxx} \frac{\partial^2 u}{\partial x^2} \approx \frac{ u(x+\Delta x,t) - 2u(x,t) + u(x- \Delta x,t)}{\Delta x^2},\\ \label{eqn:ut} \frac{ \partial u} {\partial t} \approx \frac{u(x, t+\Delta t) - u(x, t)}{\Delta t}. \end{gather}$$

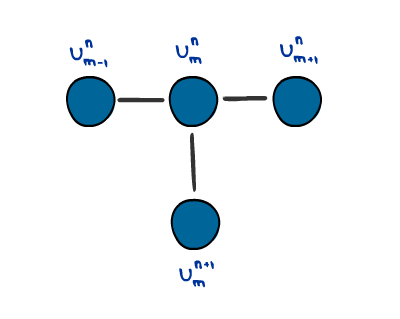
This finite difference method is also known as the Forward-Time Central-Space method, because at each iteration we approximate the value of u by considering considering the change in space centered around a point in space $x$ using values at $x\pm\Delta x$, and the change in time as in the forward Euler method. If you were to do it manually you would have a “T-shaped stencil” that you could move accross the discretized 1D rod to find the values at the next time step as shown in the figure below.

Let $n$ be the index for the time steps, and $m$ be the index for position. We'll also use $k = \Delta t$ and $h = \Delta x$, and write $u(m,n) = u_m^n$

Then, we can solve the heat equation numerically by using: $$\begin{align} \frac{1}{k} \left(u_m^{n+1} - u_m^n\right) &= \frac{1}{h^2}\left(u_{m-1}^n -2u_m^n + u_{m+1}^n\right)\\ u_m^{n+1} &= u_m^n+\frac{k}{h^2} \left(u_{m-1}^n -2u_m^n + u_{m+1}^n\right)\\ \label{eqn:forNum} u_m^{n+1} &= \frac{k}{h^2} u_{m-1}^n +\left(1-\frac{2k}{h^2}\right)u_m^n + \frac{k}{h^2}u_{m+1}^n. \end{align}$$

What happens at the edges?

Let us discretize our rod at $M$ points, $u_1^n, u_2^n,..., u_{M-1}^n, u_{M}^n$. Notice that stencil will work at every position along a one-dimensional rod except for the two edges (at $u_1$ and $u_M$), because we have no a priori values for $u_0$ and $u_{M+1}$ to approximate the centered finite difference. We can work around this by using the fact that we applied periodic boundary conditions. This means that $u_1^n = u_M^n$, so: $$\begin{gather} u_{0}^n = u_{M-1}^n, \\ u_{M+1}^n = u_2^n \end{gather}$$

If you use MATLAB to program the numerical solution to the 1D Heat Equation, it is convenient to rewrite $\eqref{eqn:forNum}$ as a matrix operation, $$\begin{equation} \label{eqn:diffFor} \vec{u}^{n+1} = B \vec{u}^n, \end{equation}$$ where $\vec{u}^n$ are the values of $u$ at time $n$ for all values $x_1,...,x_M$, and $$\begin{equation} \label{matrix} B = \left(\begin{array}{cccccc} a&b&0&\dots&b&0\\ b&a&b&\dots&0&0 \\ 0&b&a&\ddots& & 0\\ 0&&\ddots&\ddots& \ddots &\vdots\\ \vdots& & & b & a &b \\ 0 & b & \dots & 0 & b&a \end{array}\right) , \end{equation}$$ where $a = 1-\frac{2k}{^2}$, and $b= \frac{k}{h^2}$, and where B is a tridiagonal matrix except at $B_{1,M-1} = B_{M, 2} = b$ that satisfies the boundary conditions.

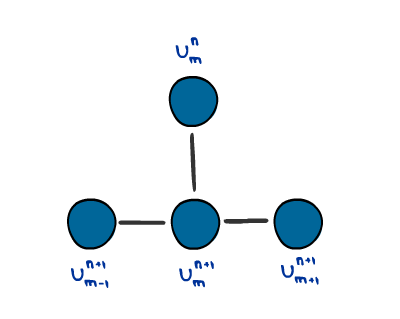
The forward method works well, but is not guaranteed stability. Implicit methods are guaranteed stability which will allow you to take larger time steps without getting unrealistic results (although beware that “realistic” does not imply “accurate”).

The idea is the same, but our “T-shaped stencil” is now flipped upside down, and we get, $$\begin{align} \frac{1}{k} \left(u_m^{n+1} - u_m^n\right) &= \frac{1}{h^2}\left(u_{m-1}^{n+1} -2u_m^{n+1} + u_{m+1}^{n+1}\right)\\ \label{eqn:forNum2} u_m^{n} &= -\frac{k}{h^2} u_{m-1}^{n+1} +\left(1+\frac{2k}{h^2}\right)u_m^{n+1} - \frac{k}{h^2}u_{m+1}^{n+1}. \end{align}$$

We can write it as a product of matrices to get $$\begin{equation} \label{impEqn} \vec{u}^n = B'\vec{u}^{n+1}, \end{equation}$$ where $B'$ has the same form as $B$ in $\eqref{eqn:forNum}$ but with $a = 1+\frac{2k}{h^2}$ and $b=-\frac{k}{h^2}$

Then, at each step we need to solve Equation $\eqref{impEqn}$ for $\vec{u}^{n}$ so: $$\begin{equation} \vec{u}^{n+1} = B'^{-1} \vec{u}^n \end{equation}$$

Let us now see how to update our value of $u$, when we are looking at a Reaction-Diffusion system like, $$\begin{equation} \frac{\partial u}{\partial t} = D\frac{\partial^2 u}{\partial x^2} + f(u). \end{equation}$$

Recall that if we just had, $$\begin{equation} \frac{\partial u}{\partial t} = f(u), \end{equation}$$ then we simulate it using the forward Euler method so, $$\begin{equation} \label{eqn:reaction} \vec{u}^{n+1} = f(\vec{u}^n) \, k. \end{equation}$$ where $k = \Delta t$.

Therefore, for the explicit method, we combine $\eqref{eqn:diffFor}$ and $\eqref{eqn:reaction}$ to obtain that the update at each time step is, $$\begin{equation} \vec{u}^{n+1} = B \,\vec{u}^n + f(\vec{u}^n)\, k \end{equation}$$

If we use the implicit method for the diffusion, and the explicit method, then we need to solve $$\begin{equation} B' \, \vec{u}^{n+1} = \vec{u}^n + f(\vec{u}^n)\, k, \end{equation}$$ for $\vec{u}^{n+1}$. As a result we get that at each step we need to compute, $$\begin{equation} \vec{u}^{n+1} = B'^{-1} \,(\vec{u}^n + f(\vec{u}^n)\, k). \end{equation}$$

First, take a look at the following screencast. You can find all of the relevant Matlab code below so that you can play around with it on your own.

This code was used in the screencast above.

%%%%%%%%%%%%%%%%%%%%%%%
%%% Screencast code %%%
%%%%%%%%%%%%%%%%%%%%%%%
 
 
%%% Forward Finite difference method %%%
 
% At each time step compute: u(n+1) = B u(n)
% How do we create B in MATLAB?
 
% Parameters
D = 2;               % Diffusion constant
dx = 0.2; dt = 0.1;  % space and time step
Nx = 6;              % Number of grid points
 
% Making the Matrix
a = (1-2*D*dt/dx^2); % Diagonal values
b = D*dt/dx^2;       % Off-diagonal values
main = a*sparse(ones(Nx,1)); 
off  = b*sparse(ones(Nx-1,1));
B = diag(main) + diag(off,1) + diag(off,-1); % Make B
% Apply periodic boundary conditions
B(1, end-1) = b; 
B(end, 2) = b;
 
 
% Useful MATLAB functions we used
    % diag 
    % imagesc 
    % sparse

This code will create the plots that were used to make the animations shown in Turing II.

% The Mathematics of Patterns 2013
% Turing Instabilities II: Gierer Meinhardt system in 1D
 
% This MATLAB code will show you how to numerically simulate the 1D Gierer
% Meinhardt system, and make the (simplified) version of the animations in
% the Turing Instabilities II section of the website. 
clear all
close all
 
%%%%%%%%%%%%%%%%%%%%%
%%%    Set-up     %%%
%%%%%%%%%%%%%%%%%%%%%
 
% Parameter values
bc  = 0.35; 
Du = 1;   Dv = 30;  % Diffusion constants
 
% Grid and initial data:
% w = 10;  %no pattern 
w = 80;  % pattern
 
Nx = 500; % How many points we want to discretize our domain with
x = linspace(0,w, Nx); 
dx = x(2) - x(1); 
 
dt = 1; % size of our time step
t = 0:dt:400;   
Nt = length(t); % Number of time points
 
% Set up for the surface 
[X, T] = meshgrid(x, t); 
U = 0*X;
V = 0*X;
 
% Easier to deal with column vectors
x = x(:);
t = t(:);
 
%Initial conditions: small perturbation away from steady state
u = 1/bc*ones(length(x),1) + 0.01*rand(Nx, 1); 
v = 1/bc^2*ones(length(x),1);
 
% Save initial conditions
U(1,:) = u;
V(1,:) = v;
 
 
%%%%%%%%%%%%%%%%%%%%%%%%%
%%% Making the matrix %%%
%%%%%%%%%%%%%%%%%%%%%%%%%
 
% To begin, let us recall how to set up the matrices used in the explicit
% and implicit finite difference methods.
 
 
%%% Forward (explicit) method %%%
% We want a tridiagonal matrix (see notes for details) 
a = (1-2*Du*dt/dx^2);  % values along the diagonal
b = Du*dt/dx^2;        % values in the off-diagonal
main = a*sparse(ones(Nx,1)); 
off  = b*sparse(ones(Nx-1,1));
Bu = diag(main) + diag(off,1) + diag(off,-1); %Still a sparse matrix
% Satisfying boundary conditions
Bu(1, end-1) = b; 
Bu(end, 2) = b;
 
% To have a more numerically stable code, we use the implicit method. 
 
%%% Backward (implicit) method %%%
% For u
    a = (1+2*Du*dt/dx^2);  % values along the diagonal
    b = Du*dt/dx^2;        % values in the off-diagonal
    main = a*sparse(ones(Nx,1)); 
    off  = -b*sparse(ones(Nx-1,1));
    Bu = diag(main) + diag(off,1) + diag(off,-1); %Still a sparse matrix
    % Satisfying boundary conditions
    Bu(1, end-1) = -b; 
    Bu(end, 2) = -b;
 
% Same thing for v
    a = (1+2*Dv*dt/dx^2); b = Dv*dt/dx^2;
    main = a*sparse(ones(Nx,1));
    off  = -b*sparse(ones(Nx-1,1));
    Bv = diag(main) + diag(off,1) + diag(off,-1);
    Bv(1, end-1) = -b;
    Bv(end, 2) = -b;
 
%%%%%%%%%%%%%%%%%%%%%%%%%
%%%     Plotting      %%%
%%%%%%%%%%%%%%%%%%%%%%%%%
 
figure(1); %create new figure
plot(x,u,'g.-', 'linewidth',1);
hold on;
plot(x,v,'r.-', 'linewidth',1);
hold off;
 
axis([-1 80 -.01 15.01])  % Fix axis limits
 
for j = 1:Nt
    % f and g are the reaction terms in the G-M system
    f = u.^2./v-bc*u;
    g = u.^2 - v;
 
    % At each step we need to solve the system
    u = Bu\(u + dt*f);   % backward Euler
    v = Bv\(v + dt*g);
    
    % Plot
    plot(x,u,'g.-', 'linewidth',1);
    hold on;
    plot(x,v,'r.-', 'linewidth',1);
    hold off;
    axis([-1 80 -.01 15.01])
    title(['t = ', num2str(j*dt)],'fontsize',24)
    drawnow; 
    
    % Save for surface
    U(j,:) = u;
    V(j,:) = v;
end
 
 
%%%% Plotting the surface %%%%
figure(2);
s = surf(x, t, U)
set(s, 'EdgeColor', 'none', 'FaceColor', 'interp'); % Sets up the colors
xlabel('x') 
ylabel('t') 
zlabel('u')
 
%%%% contour plot %%%
figure(3);
p = pcolor(x, t, U);
set(p, 'EdgeColor', 'none', 'FaceColor', 'interp');

• Home
• Pattern formation in nature
• Reaction-diffusion I
• Reaction-diffusion II
• Turing I
• Turing II
• Turing III
• Numerical methods and Matlab
• Videos
• About