Table of Contents
Turing Instabilities and Tiger stripes
All of the sections up until now have been building up the mathematical foundations that we need to answer the question I asked at the very beginning: Where do tigers get their stripes?
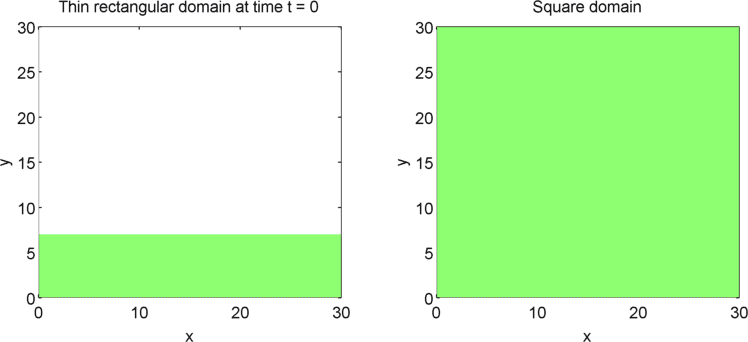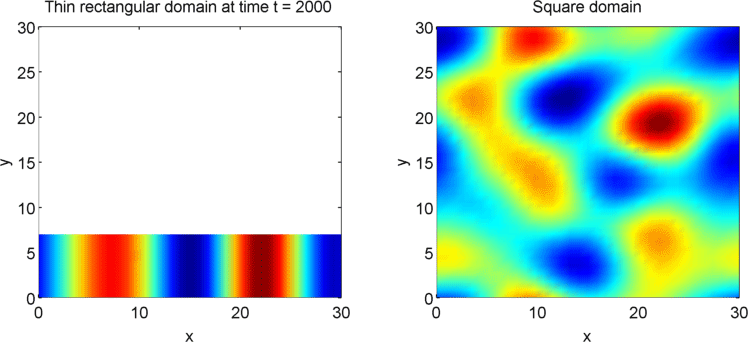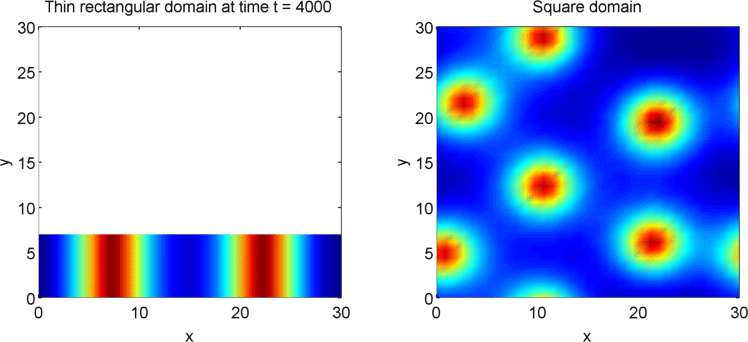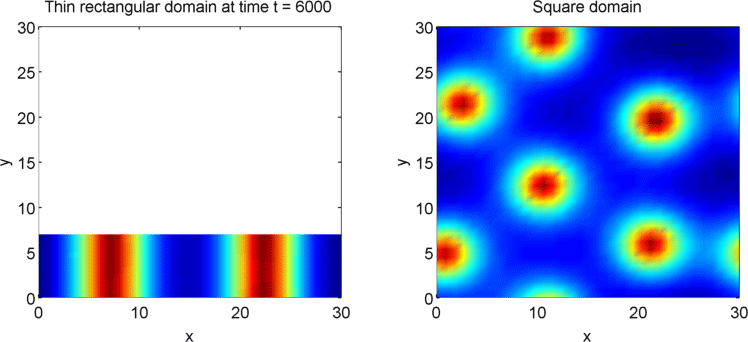
The systems that we have considered so far are all one-dimensional, but it is not difficult to extend our analysis into two dimensions. We can revisit the idea of spatial dependence of patterns with the 2D Gierer Meinhardt model on a thin domain and on a square domain.
Keeping all other parameters the same except for the width, we obtain stripes on a thin domain with periodic boundary conditions, and spots on the square domain. Recall from the previous section that there was a minimum domain size for the Gierer Meinhardt system to have patterns. In the thin domain case, we find that the short edge is not long enough to have patterns, so we only get patterns in one direction which we see as stripes. On the other hand, in the square domain, we get patterns in both directions which results in spots with the parameters used.
What connection can this have with animal coats? Murray ran simulations of reaction diffusion models on cylindrical domains that tapered off at the ends. (i.e. on a trapezoidal surface with periodic boundary conditions on the legs and zero-flux boundary conditions on the bases), and saw that you could get tails that were either entirely striped or that had spots that became stripes at the tip of the tail, similar to the markings observed on the tails of different felines ([(murray_1988)], 3.1 in [(murrayBook_1989)]). This phenomenological model is exciting because it suggests that if coat patterns are due to the reaction between two (or more) chemical species, the same biological mechanism can result in different patterns (eg. fully striped genet tails and half-spotted half-striped jaguar tails) due to the different sizes of the tails during development [(murray_1981)].
Beyond Turing and stripes
Not all reaction-diffusion systems generate patterns through the same mechanism that was originally proposed by Alan Turing. In addition, small changes in parameters other than just the spatial domain can lead to very different patterns. For example, a very famous system of reaction diffusion equations are the Gray-Scott (GS) equations, which simulate an activator-substrate system; the reaction can be written as:
\begin{gather} \label{eqn:gsReaction1} u+2v \rightarrow 3v, \\ \label{eqn:gsReaction2} v \rightarrow p. \end{gather}
Unlike the Gierer-Meinhardt model which had one chemical acting as an activator, and the other chemical as an inhibitor, the GS system has two chemicals $u$ and $v$, where $v$ is transformed to an inert product (or substrate) $p$, and $u$ and $v$ react together to produce more $v$.
The evolution of the concentration of $u$ and $v$ are described by,
\begin{gather} \label{eqn:gsor1} \frac{\partial u}{\partial t} = D_u \frac{\partial^2u}{\partial x^2} - uv^2 +F(1-u), \\ \label{eqn:gmor2} \frac{\partial v}{\partial t} = D_v \frac{\partial^2v}{\partial x^2}+uv^2-(F+c)v. \end{gather} where $D_u$, $D_v$ are the diffusion constants as usual, and $F$, $c$ are constants.
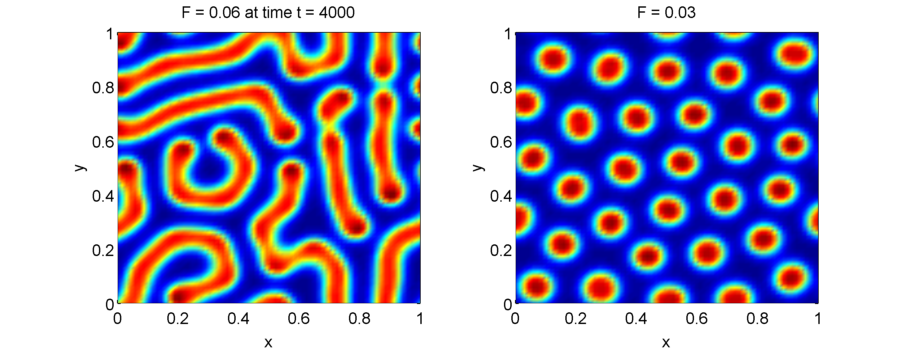
Simulations of the Gray-Scott equations can lead to very different patterns using slightly different parameters as shown below. (For a more complete map of parameter-to-patterns see Xmorphia).
Note that the Gray-Scott equations lead to much more complicated dynamics than the Turing systems, and the patterns that you see are due to the nonlinear interactions between $u$ and $v$.
To learn more about Ready click here. You can download a working version for free and play with some of the cool patterns and meshes that they have created.
The biology in the math
As we covered in the introduction, the assumption that many of the pattern formation models we covered above make is that patterning of organisms occur via the spatial pre-patterning of chemical concentrations that occur during development. As a result, many models have been extended to study patterns in growing domains [(maini_2012)].
In addition, many variations of reaction diffusion equations have been developed to model different coat patterns in nature including:
- Fish (see [(kondo_2009)], [(nakamasu_2009)])
- Snakes (see [(murrayMyerscough_1991)] )
- Leopards (see [(murray_1988)] and chapter 3 [(murrayBook_1989)] )
The purpose of mathematical models are to reach a deeper understanding of the complex phenomena seen in nature, so all models, by definition, are false. However, one of the biggest criticisims that the mathematical models for pattern formation have received is that they are “too false”, because they are all phenomenological and have little experimental evidence that makes the reaction-diffusion model biologically plausible. The reaction-diffusion models we have studied in these notes have a lot of attractive points (eg. they generate the right patterns, and relatively simple equations can lead to a great variety of patterns with small parameter changes). However, even though we obtain the patterns we observe in nature, this does not mean that we have captured the biological mechanism at work. There is a good example of the heated debates that can ensue regarding the plausibility of mathematical models in the book, Modeling Differential Equations in Biology [(taubes_2001)]. Here, Taubes presents a series of three articles discussing a reaction-diffusion model for the formation of patterns in angelfish that disagree on the applicability of the model, and alternatives that would yield similar results.
Our knowledge about the science behind pattern formation has been slower to develop than the creation of mathematical models. In part, this is due to the fact that it is hard to isolate individual molecules and study their role in biological mechanisms. Many of the pattern formation models we have discussed assume that there exist chemicals in developing embryos that will react in certain ways, but it is much easier to posit the existence of such chemicals than to find them, isolate them, and test that they do what the models predict. In the end, it is not enough to have just the experiments or just the math. Mathematical models can help shape and direct the experimental design, and the results can then be used to update, change or discard the model.
References
[(:maini_2012» author: Maini PK, Wooley TE, Baker RE, Gaffne EA, and Lee SS ref-author: Maini et.al title: Turing's model for biological pattern formation and the robustness problem journal: Interface Focus year: 2012 )]
[(:kondo_2009» author: Kondo S, Iwashita M, Yamaguchi M ref-author: Kondo et al title: How animals get their skin patterns: fish pigment pattern as a live Turing wave journal: Int J Dev Biol year: 2009 volume: 53 )]
[(:nagorka_1992» author: Nagorka BN and Mooney JR ref-author: Nagorcka and Mooney title: From stripes to spots: Prepatterns which can be produced in the skin by a reaction-diffusion system journal: IMA Journal of Mathematics Applied in Medicine and Biology year: 1992 volume: 9 )]
[(:nakamasu_2009» author: Nakamasu A, Takahashi G, Kanbe A, and Kondo S ref-author: Nakamasu et. al. title: Interactions between zebrafish pigment cells responsible for the generation of Turing patterns journal: PNAS volume: 106 number: 21 year: 2009 )]
[(:murray_1988» author: Murray, J.D. ref-author: Murray title: Mammalian coat patterns: How the leopard gets its spots journal: Scientific American volume: 256 number: 3 year: 1988 )]
[(:murray_1981» author: Murray, J.D. ref-author: Murray title: A pre-pattern formation mechanism for animal coat markings journal: J. Theor. Biol. volume: 88 number: 1 year: 1981 )]
[(:murrayBook_1989» author: Murray, J.D. ref-author: Murray title: Mathematical Biology II: Spatial models and biomedical applications publisher: Springer year: 1989 )]
[(:murrayMyerscough_1991» author: Murray, J.D and Myerscough M.R. ref-author: Murray and Myerscough title: Pigmentation pattern formation on snakes journal: J. Theor. Biol. volume: 149 year: 1991 )]
[(:taubes_2001» author: Taubes CH ref-author: Taubes title: Modeling Differential Equations in Biology publisher: Cambridge University Press year: 2001 )]