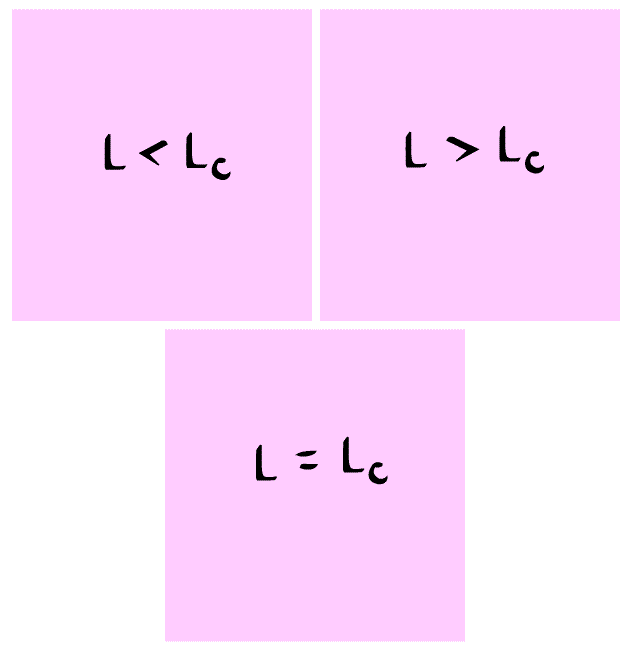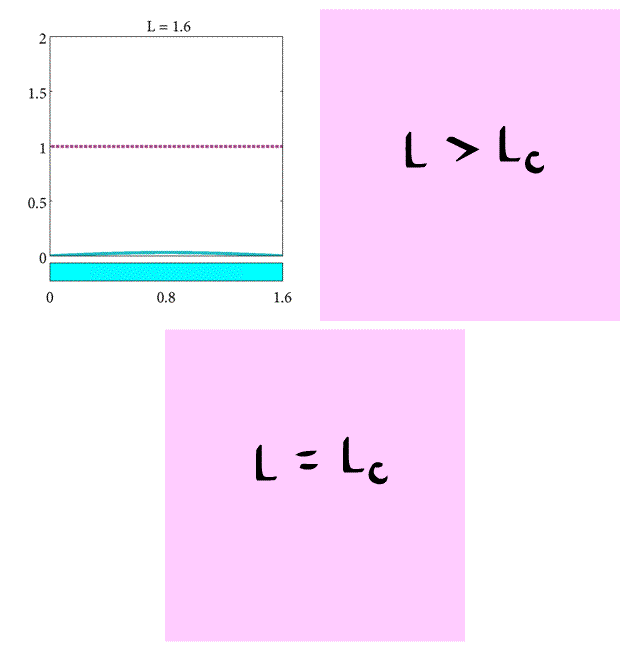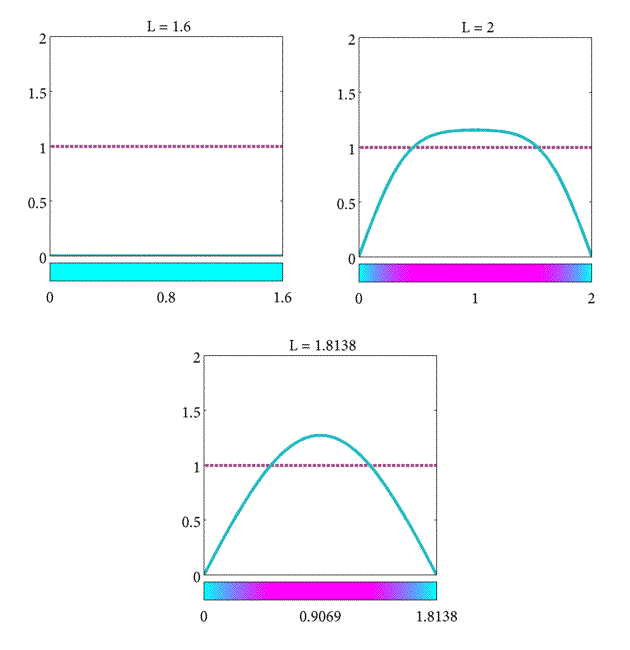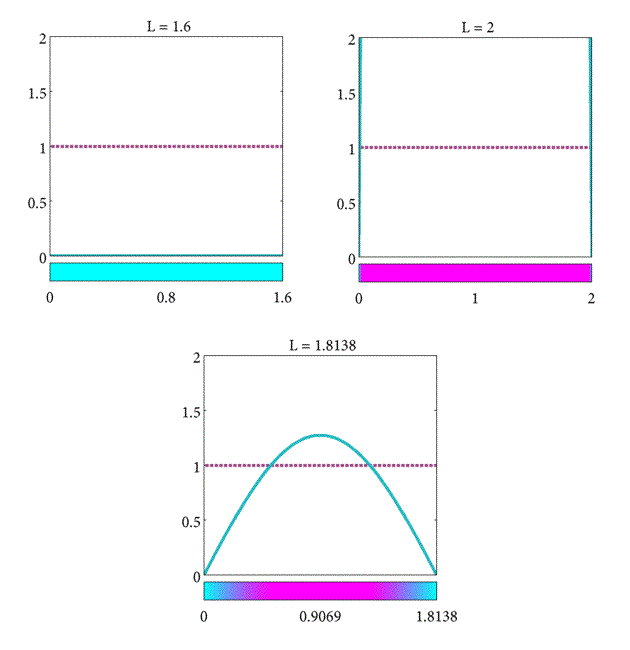Table of Contents
Reaction-Diffusion Equations 2
Why do we need Diffusion AND Reactions?
What benefit do diffusion-reaction models have over just reaction or just diffusion models?
As discussed in the introduction, one of the big questions in developmental biology is how complex organisms emerge from a single fertilized egg. The answer has long been thought to be chemical gradients. If you have different chemicals at different concentrations throughout the embryo, and you apply a threshold function so that the cell differentiates depending on the chemicals immediately surrounding it, then you get a spatially organized differentiation of cells that will later develop into different organs and body parts.
The question of how these gradients are set up were subject of great debate, and at the beginning, diffusive models were discarded because it was assumed to be too slow to establish a stable gradient. In 1970, Francis Crick (who would later win the Nobel Prize for discovering DNA) proposed that diffusion was a plausible mechanism since it was fast enough. [(crick_1970)]
He modeled this as a one-dimensional diffusion problem much like the example above. In other words, he imagined an embryo as a line of cells. His equation was,
\begin{equation} \label{eqn:Crick1} \frac{\partial C(x,t)}{\partial t} = D \frac{ \partial^2C(x,t)}{\partial x^2}, \end{equation} where $C(x,t)$ is the concentration of the chemical at position x and time t. Furthermore, he placed boundary conditions $C(0,t) = C_0$ and $C(L,t) = 0$, where L is the length of the embryo.
Crick wanted a stable gradient (in time), so he solved \eqref{eqn:Crick1} by setting the LHS to zero. The system becomes \begin{equation}\label{eqn:Crick2} \frac{\partial^2 C(x,t)}{\partial x^2} = 0, \end{equation} which implies that the concentration gradient will be a straight line when it is stable.
He then verified that the stable linear gradient would be set up fast enough. Diffusion is a random walk process and our derivation above showed that the diffusion constant has dimensions $L^2t^{-1}$. The time it takes to set up the gradient is, \begin{equation} \label{eqn:Crick3} t - \frac{A(nl)^2}{D}, \end{equation} where $t$ = time in seconds, $n$ = number of cells in the embryo, $l$ = length of each cell in cm, and $D$ = diffusion constant in $cm^2s^{-1}$. $A$ is a numerical constant that is fit from data. Assuming that the time it takes a real embryo to set up the chemical gradient is around three hours, Crick found that diffusion would be fast enough if L was on the order of milimeters, which is the case with fruit flies.
Crick did not have the tools to check whether the concentration gradient of bicoid in fruit fly embryos was linear, so he was satisfied with using just diffusion. He also used boundary conditions without stating what could biologically explain the $u(L,t)=0$ condition.
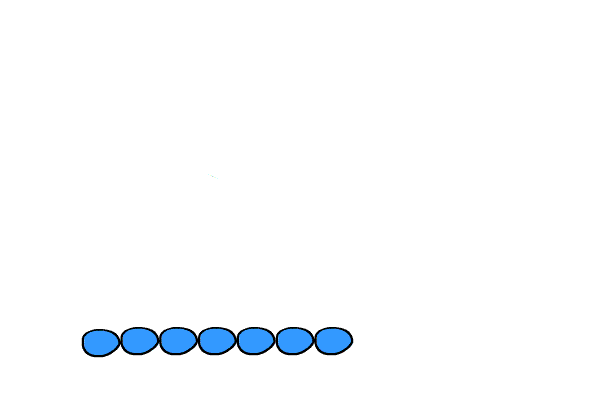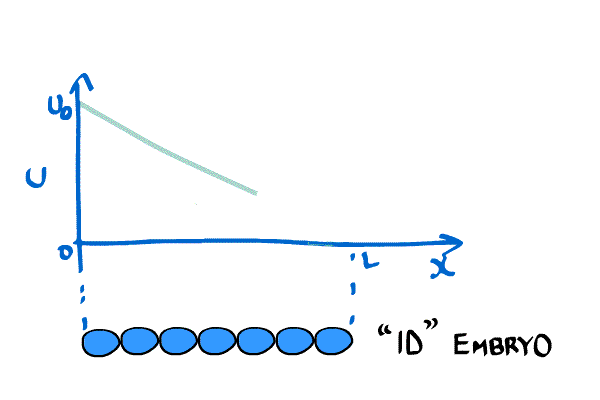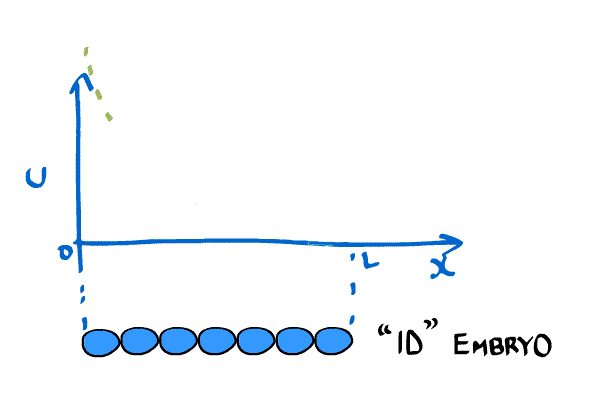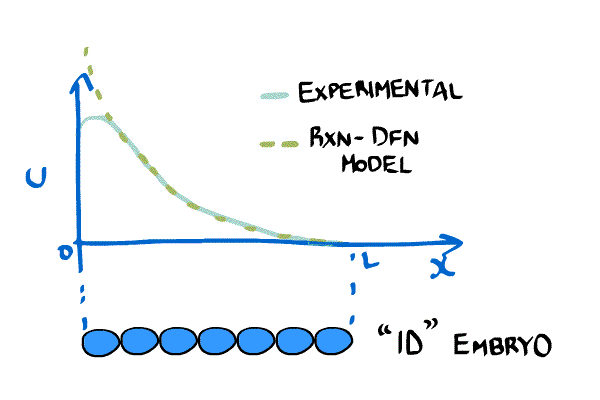
New imaging technologies have been developed that allow scientists to measure the concentration of chemicals in embryos. One very important chemical is called bicoid and it is important in establishing an asymmetry in the anterior-posterior axis (i.e. it determines what cells become part of the head and which ones become part of the body). The bicoid gradient can be approximated by an exponential curve.
Instead of relying solely on boundary conditions like Crick, models of bicoid have introduced a reaction term. Bicoid will take time both to get produced, and once it is created it degrades naturally. This new model looks like: \begin{equation} \label{eqn:revMod1} \frac{\partial C(x,t)}{\partial t} = D(t) \frac{ \partial^2C(x,t)}{\partial x^2} - \frac{1}{\tau}C(x,t) + \rho(x,t), \end{equation} where $D$ is the diffusion constant, $\tau$ is the degradation rate, and $\rho$ is a synthesis rate [(little_2011)]
Consider a simpler version of \eqref{eqn:revMod1}, \begin{equation} \label{eqn:revMod2} \frac{\partial C(x,t)}{\partial t} = D \frac{ \partial^2C(x,t)}{\partial x^2} - \frac{1}{\tau}C(x,t), \end{equation} which we can solve for a stable gradient analytically, \begin{equation} \label{eqn:revMod3} C(x,t) = C_0 e^{-x/\lambda},\quad \lambda = \sqrt{D\tau} \end{equation}
This example shows why sometimes reaction and diffusion are needed to make realistic biological models. Diffusion can model spatial phenomena, but often, like in the case of bicoid, we have local reactions that can only be included in the model with equations like the Reaction-Diffusion PDE in \eqref{eqn:revMod1}.
Reaction-Diffusion equations and spatial domains
So far we have seen how reaction and diffusion can work together to create biological models, and how diffusion is really fast in short length scales. However, we have not studied the spatial properties of Reaction-Diffusion equations.
Let us consider one last example of a one-dimensional reaction diffusion equation to study the effect of the spatial domain on the structure that emerges [(kierstead_1953)]. Imagine we have a phytoplankton population and it can only survive in some water mass that has the adequate temperature and dissolved nutrients. If the water mass is isolated (i.e. surrounded by water where the phytoplankton will die), is there a minimum water mass size so that the phytoplankton population can increase?
In the ocean, this water mass would be three-dimensional, but let us take a simpler one-dimensional approach in which we consider a mass of water that has been stretched out into a very thin tube. We impose boundary conditions on the concentration of phytoplankton $c$ such that any phytoplankton at the edges are automatically destroyed, and also that the concentration is constant at $t = 0$. That is, we have \begin{gather} c(0,t) = 0 = c(L,t) \label{bcplank} \\ c(x, 0) = c_0. \label{icplank} \end{gather}
Phytoplankton cannot swim against the current of the ocean, so its motion can be described by diffusion. Therefore, if the phytoplankton population does not grow or decrease, its concentration will be the solution to the diffusion equation, \begin{equation} \label{eqn:Plank1} \frac{\partial c}{\partial t} = D \frac{\partial^2c}{\partial x^2}. \end{equation}
However, phytoplankton are living organisms, so they will reproduce at a rate that is proportional to their concentration. Therefore we add a constant term to Equation \eqref{eqn:Plank1}, \begin{equation} \label{eqn:Plank2} \frac{\partial c}{\partial t} = D \frac{\partial^2c}{\partial x^2} +Kc, \end{equation} where K is a growth constant.
Before we solve this via separation of variables, we can simplify our problem by scaling out the diffusion-less exponential growth, \begin{equation} \label{eqn:Plank3} c(x, t) = f(x, t)e^{Kt}, \end{equation}
and substituting Equation \eqref{eqn:Plank3} into Equation \eqref{eqn:Plank2}, we find that f must satisfy the standard diffusion (or heat) equation of the previous part, \begin{equation} \label{eqn:Plank4} \frac{\partial f}{\partial t} = D \frac{\partial^2f}{\partial x^2}. \end{equation}
By the standard techniques of Fourier series, and using the boundary conditions of $c = 0$ and $x = 0, L$, we find that \begin{equation} \label{eqn:Plank5} f = \sum_{n=1}^\infty B_n \sin \left(\frac{n\pi x}{L}\right) e^{-n^2\pi^2D/L^2t}, \end{equation}
where $B_n$ are the Fourier sine coefficients given by, \begin{equation} \label{eqn:Plank6} B_n = \frac{2}{L} \int_0^L c_0 \sin \left(\frac{n\pi x}{L}\right) \, \de{x}, \end{equation}
for $n = 1, 2, \ldots$, which are then computed for given initial concentration, $c_0$.
Substituting \eqref{eqn:Plank4} into \eqref{eqn:Plank5} we get the concentration, \begin{equation} \label{eqn:Plank7} c(x,t) = \sum_{n=1}^\infty B_n \sin \left(\frac{n\pi x}{L}\right) e^{(K-n^2\pi^2D/L^2)t}. \end{equation}
What will be the steady state of the phytoplankton population?
They key is to note from \eqref{eqn:Plank7} that because the Fourier coefficients are bounded and decreasing as $n \to \infty$, and since the sinusoidals are well behaved, the long term behavior of the system will be controlled by the time term in Equation \eqref{eqn:Plank7}, \begin{equation} \label{eqn:Planktime} e^{(K-n^2\pi^2D/L^2)t}. \end{equation}
The sign of the argument of the exponential will determine whether the population of the plankton will grow, stay the same or decay as time goes to infinity. Thus, we obtain three cases related to the argument of \eqref{eqn:Planktime}:
- If the argument is exactly zero, then the population will stay the same.
- If the argument is negative, then the population will decay over time.
- If the argument is positive, then the population will grow over time.
Moreover, if these conditions hold for the $n=1$ mode, then the $n = 2, 3,$… higher modes don't change the steady-state behaviour. For $n = 1$, the bifurcation (the point at which the behavior changes from decay to growth) is found at the length, $L$ such that \begin{equation} \label{eqn:Plank8} K - \pi^2\frac{D}{L^2} = 0, \end{equation}
and thus, we can obtain a critical length given by \begin{equation} \label{eqn:Plank10} L_c = \pi\sqrt{\frac{D}{K}}. \end{equation}
In summary, we have found the critical length of the domain such that
- If $L= L_c$ the population will stay the same.
- If $L>L_c$ the population will increase.
- If $L<L_c$ the population will decrease.
As a final note, observe that the critical length increases proportional to D but inversely proportional to K. This suggests that the steady-state behavior of the plankton population is determined by the relative strength of the diffusive and reactive terms in Equation \eqref{eqn:Plank2}. When $L>L_c$ then the reactive term $Kc$ will dominate the long-term behavior, but when $L<L_c$ the diffusive term $D\frac{\partial^2c}{\partial x^2}$ dominates. When $L = L_c$ the diffusive and reactive forces balance each other equally. (For a more complete discussion on the minimum domains for spatial patterns refer to [(murraySperb_1983)]).
You can now proceed to the next chapter: Turing Instabilities I
References
[(:crick_1970» author: Crick, F. ref-author: Crick title: Diffusion in Embryogenesis journal: Nature volume: 225 year: 1970 )]
[(:einstein_1956» author: Einstein, A. ref-author: Einstein publisher: Dover Publications title : Investigations on the Theory of the Brownian Movement year : 1956 )]
[(:mehrer_2009» author: Mehrer, H. and Stolwijk, N.A. ref-author: Mehrer and Stolwijk title: Heroes and Highlights in the History of Diffusion journal: Diffusion Fundamentals volume: 11 number: 1 year: 2009 )]
[(:nelson_1967» author : Nelson, E. ref-author: Nelson publisher : Princeton University Press title : Dynamical theories of Brownian motion year : 1967 )]
[(:little_2011» author: Little, SC, Tkacik G, Kneeland TB, Wiechaus EF, Gregor T ref-author: Little et al title: The Formation of the Bicoid Morphogen Gradient Requires Movement from Anteriorly Localized mRNA journal: PLoS Biology volume: 9 number: 3 year: 2011 )]
[(:kierstead_1953» author: Kierstead, H, and Slobodkin LB. ref-author: Kierstead and Slobodkin title: The size of water masses containing plankton blooms journal: J. Mar. Res volume: 12 number: 1 year: 1953 )]
[(:murraySperb_1983» author: Murray J.D. and Sperb R.P. ref-author: Murray and Sperb title: Minimum domains for spatial patterns in a class of reaction diffusion equations journal: J. Math. Biology volume: 18 year: 1983 )]